B-Trees (NTFS)
B-Trees
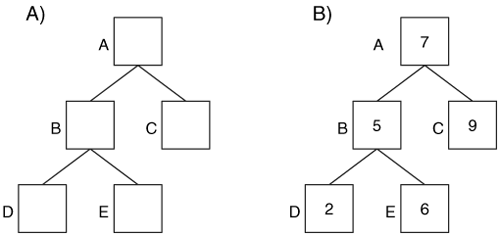
An NTFS index sort attributes into a tree, specifically a B-tree. A tree is a group of data structures called nodes that are linked together such that there is a head node and its branches out to the other nodes. Consider Figure 11.13(A), where we see node A on top and it links to nodes B and C. Node B links to nodes D and E. A parent node is one that links to other nodes, and a child node is one that is linked to. For example, A is a parent node to B and C, which are children of A. A leaf node is one that has no links from it. Nodes C, D, and E are leaves. The example shown is a binary tree because there are a maximum of two children per node.
Figure 11.13. Examples of A) a tree with 5 nodes and B) the same tree that is sorted by the node values
Trees are useful because they can be used to easily sort and find data. Figure 11.13(B) shows the same tree as we saw on the left side, but now with values that are assigned to each node. If we are trying to look up a value, we compare it to the root node. If the root node is larger, we go to the child on the left. If the root node is smaller, we go to the child on the right. For example, if we want to find the value 6, we compare it to the root value, which is 7. The node is larger, so we go to the left-hand child and compare its value, which is 5. This node is smaller, so we go to the right-hand child and compare its value, which is 6. We have found our value with only three comparisons. We could have found the value 9 in only two comparisons instead of five if the values were in a list.
NTFS uses B-trees, which are similar to the binary tree we just saw, but there can be more than two children per node. Typically, the number of children that a node has is based on how many values each node can store. For example, in the binary tree we stored one value in each node and had two children. If we can store five values in each node, we can have six children. There are many variations of B-trees, and there are more rules than I will describe here because the purpose of this section is to describe their concepts, not to describe how you can create a B-tree.
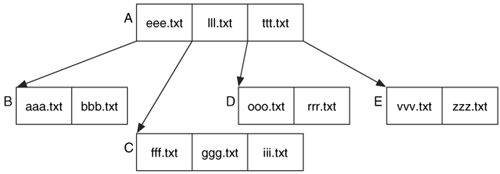
Figure 11.14 shows a B-tree with names as values instead of numbers. Node A contains three values and four children. If we were looking for the file ggg.txt, we would look at the values in the root node and determine that the name alphabetically falls in between eee.txt and lll.txt. Therefore, we process node C and look at its values. We find the file name in that node.
Figure 11.14. A B-tree with file names as values.
Now let's make this complex by looking at how values are added and deleted. This is an important concept because it explains why deleted file names are difficult to find in NTFS. Let us assume that we can fit only three file names per node, and the file jjj.txt is added. That sounds easy, but as we will see it results in two nodes being deleted and five new nodes being created. When we locate where jjj.txt should fit, we identify that it should be at the end of node C, following the iii.txt name. The top of Figure 11.15 shows this situation, but unfortunately, there are now four names in this node, and it can fit only three. Therefore, we break node C in half, move ggg.txt up a level, and create nodes F and G with the resulting names from node C. This is shown at the bottom of Figure 11.15.
Figure 11.15. The top tree shows 'jjj.txt' added to node C, and the bottom tree is the result of removing node C because each node can have only three names.
Unfortunately, node A now has four values in it. So we divide it in half and move ggg.txt to the top-most node. The final result can be found in Figure 11.16. Adding one file results in removing nodes A and C and adding nodes F, G, H, I, and J. Any remnant data in nodes A and C from previously deleted files may now be gone.
Figure 11.16. The final state from adding the 'jjj.txt' file.
Now delete the zzz.txt file. This action removes the name from node E and does not require any other changes. Depending on the implementation, the details of zzz.txt file may still exist in the node and could be recovered.
To make things more difficult, consider if fff.txt was deleted. Node F becomes empty, and we need to fill it in. We move eee.txt from node I to node F and move bbb.txt from node B to node I. This creates a tree that is still balanced where all leaves are the same distance from node H.
The resulting state is found in Figure 11.17.
Node B will contain bbb.txt in its unallocated space because bbb.txt was moved to node I. Our analysis tool might show that the bbb.txt file was deleted, but it really wasn't. It was simply moved because fff.txt was deleted.
The point of walking through the process of adding and deleting values from the tree was to show how complex the process could be. With file systems, such as FAT, that use a list of names in a directory, it is easy to describe why a deleted name does or does not exist, but with trees it is very difficult to predict the end result.
REF- File System Forensics Analysis (BRAIN CARRIER) (2005)



Comments